순열과 조합
순열
순열(順列, permutation)은 서로 다른 n개의 원소를 가지는 어떤 집합에서 중복 없이 순서에 상관있게 r개의 원소를 선택하거나 혹은 나열하는 것이며, 이는 조합과 마찬가지로 n개의 원소로 이루어진 집합에서 r개의 원소로 이루어진 부분집합을 만드는 것과 같다.


순열은 조합과 달리 순서도 따져서 부분집합을 만들기 때문에 사과가 뒤로 가는 경우와 사과가 앞으로 가는 경우를 다르게 보고 각기 하나의 경우의 수로 친다. 그래서 {사과 오렌지} {오렌지 사과}가 다른 집합으로 취급된다.
순열의 식은 다음과 같다.

순열은 일반화 과정을 거쳐, Permutation의 약자 P로 표현한다. 여기서도 n은 원소의 총 개수를 의미하고, r은 그중 뽑는 개수를 의미한다. 여기서 중요한 것은, 순열은 중복을 허용하지 않기 때문에 반드시 R <= N을 만족해야 한다는 것이다. 과일이 3개가 있는데 4개, 5개를 뽑으라는 것처럼, 없는 것들을 뽑으라는 말과 똑같기 때문에 R은 최대 N개까지만 뽑을 수 있다.

조합
조합(組合, combination)은 서로 다른 n개의 원소를 가지는 어떤 집합에서 중복 없이 순서에 상관없게 r개의 원소를 선택하는 것이며, 이는 n개의 원소로 이루어진 집합에서 r개의 원소로 이루어진 부분집합을 만드는 것과 같다.


조합은 순서에 상관없이 원소를 선택해 부분집합을 만드는 것이기 때문에 사과가 뒤로 가든, 앞으로 가든 상관 없이 그저 사과 1개와 오렌지 1개가 있으면 하나의 경우의 수로 친다.
조합의 식은 다음과 같다.

조합은 일반화 과정을 거쳐, Combination의 약자 C로 표현한다. 여기서 n은 원소의 총 개수를 의미하고, r은 그중 뽑는 개수를 의미한다. 여기서 중요한 것은, 조합은 중복을 허용하지 않기 때문에 순열과 마찬가지로 반드시 R ≤ N을 만족해야 한다는 것이다.

GCD와 LCM(최대공약수와 최소공배수)
GCD와 LCM을 구하는 방식
1. 가장 작은 수들의 곱으로 나타내며 구하는 법

12와 18을 가장 작은 수의 곱으로 나타내보자. 여기서 겹치는 부분인 2와 3을 곱한 수인 6이 최대공약수이고, 6을 중심으로 2와 3을 곱해 나오는 수인 36이 최소공배수가 된다.
2. 공약수로 나누어보며 구하는 법

이번에는 공약수로 나누어보며 최대공약수와 최소공배수를 구하는 법을 알아보자. 우리는 이미 2와 3이 공약수임을 알고 있다. 해당 공약수들로 12와 18을 더이상 나눌 수 없는 수까지 나눈다. 여기서 나누는 데에 사용된 수인 2와 3을 곱하면 6이 나오고, 이 6은 최대공약수가 된니다. 그리고 나누는 데에 사용된 수와 더 이상 나눌 수 없는 수들을 곱하게 되면 36이 나오고, 이 수는 최소공배수가 된다.
3. 유클리드 호제법
GCD와 LCM 개념이 쓰이는 문제를 풀 때 가장 많이 쓰이는 유클리드 호제법에 대해 알아보자.
유클리드 호제법을 알고 있게 되면 최대공약수와 최소공배수를 구하는 모든 문제에 일단 적용해보고 시작할 수 있게 된다. 유클리드 호제법은 최대공약수와 관련이 깊은 공식이다. 2개의 자연수 a와 b가 있을 때, a를 b로 나눈 나머지를 r이라 하면 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론이다. 이러한 성질에 따라 b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나누는 과정을 반복해, 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수임을 알 수 있게 된다.
여기 2개의 자연수 a와 b가 있다. 단 a가 b보다 커야 한다는 조건(절대적 조건)이 있다. 왜냐하면 나누었을 때 음수가 나오면 안 되기 때문이다.
이제 a와 b를 나누었을 때 q와 r이 나온다. q는 몫(Quotient)을 의미하고, r은 나머지(Rest)를 의미한다. 여기서 다시 b를 r로 나눈다. 그러면 다시 몫인 q와 나머지인 r’가 나올 것이고, r을 다시 r’와 나누게 되면 언젠가 몫인 q와 나머지인 r이 0이 되는 상황이 도출이 된다. 이 때 나누는 수인 r’가 바로 최대공약수라는 의미이다.
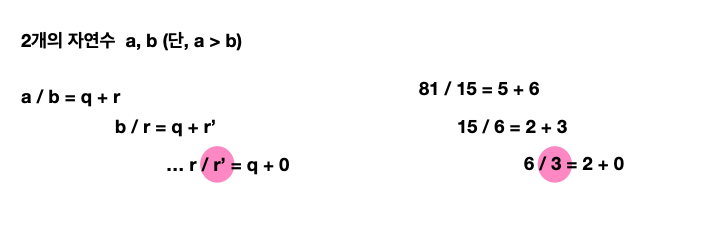
여기 81과 15가 있다. 같은 방식으로 쭉 나눴을 때, 마지막 나눗셈에서 나누는 수인 3이 최대공약수임을 확인할 수 있다. 이런 식으로 유클리드 호제법을 이용하게 되면 최대공약수를 쉽게 구할 수 있게 되고, 최대공약수를 구할 수 있게 되면 최소공배수는 자연스럽게 구할 수 있게 된다.
유클리드 호제법을 이용해 최대공약수를 구하는 로직
function gcd(a, b){
while(b !== 0){
let r = a % b;
a = b;
b = r;
}
return a;
}함수 선언을 한 뒤 a와 b를 매개변수로 받고 있으며, 그 안에 while문으로 이루어진 중심 로직이 있다. while문은 b는 0이 아니어야 함을 조건으로 받고 있는데, 모든 자연수를 0으로 나누게 되면 리턴되는 값이 Infinity이기 때문에 값이 무한대로 나오면 안되므로 해당 조건을 걸어둠으로써 값이 제대로 나오지 않는 상황을 방지해준다.
해당 조건을 지키며 b가 0이 될 때까지 계속 while문은 돌아간다. a는 b로 재할당을 시키고, b는 r로 재할당을 시키고 있다. while문이 돌아가면서 나누는 수를 재할당을 하기 때문에 마지막으로 리턴하는 값은 a가 된다.
유클리드 호제법을 이용해 최소공배수를 구하는 로직
function lcm(a, b){
return a * (b / gcd(a, b));
}해당 함수 lcm 은 마찬가지로 a와 b를 매개변수로 받고 있으며, 리턴되는 값으로 a에 b를 최대공약수로 나눈 값을 곱하고 있다. 여기서 최대공약수의 값은 위에서 만들었던 함수 gcd를 이용해 구할 수 있다. 최소공배수는 최대공약수를 이용해서 만들어지는 수이다. 그러므로 최대공약수를 만들 줄 알면 최소공배수 또한 만들 수 있게 된다.
멱집합
집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개이다. 그리고 이 모든 부분집합을 통틀어 멱집합이라고 한다. 이렇게 어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합 이라고 한다. 모든 부분집합을 나열하는 방법은 다음과 같이 몇 단계로 구분할 수 있다. 부분집합을 나열하는 방법에서 가장 앞 원소(혹은 임의의 집합 원소)가 있는지, 없는지에 따라 단계를 나누는 기준을 결정한다.
- Step A: 1을 제외한 {2, 3}의 부분집합을 나열한다.
- Step B: 2를 제외한 {3}의 부분집합을 나열한다.
- Step C: 3을 제외한 {}의 부분집합을 나열한다. → {}
- Step C: {}의 모든 부분집합에 {3}을 추가한 집합들을 나열한다. → {3}
- Step B: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열한다.
- Step C: {3}의 모든 부분집합에 {2}를 추가한 집합들을 나열하려면, {}의 모든 부분집합에 {2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {2, 3}을 추가한 집합들을 나열한다. → {2}, {2, 3}
- Step B: 2를 제외한 {3}의 부분집합을 나열한다.
- Step A: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한다.
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한다.
- Step C: {3}의 모든 부분집합에 {1}을 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 3}을 추가한 집합들을 나열한다. → {1}, {1, 3}
- Step C: {3}의 모든 부분집합에 {1, 2}를 추가한 집합을 나열하려면, {}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한 다음 {}의 모든 부분집합에 {1, 2, 3}을 추가한 집합들을 나열한다. → {1, 2}, {1, 2, 3}
- Step B: {2, 3}의 모든 부분집합에 {1}을 추가한 집합들을 나열하려면, {3}의 모든 부분집합에 {1}을 추가한 집합들을 나열한 다음 {3}의 모든 부분집합에 {1, 2}를 추가한 집합들을 나열한다.
원소가 있는지, 없는지 2가지 경우를 고려하기 때문에 집합의 요소가 n 개일 때 모든 부분집합의 개수는 2^n개 이다. 예를 들어 집합의 원소가 4개라면 모든 부분집합의 개수는 24, 집합의 원소가 5개라면 25가 된다. 간단히 {1, 2, 3}의 모든 부분집합을 구하는 단계는 다소 복잡해 보일 수 있지만 이 단계를 자세히 보면, 트리구조와 비슷한 형태라는 사실을 떠올릴 수 있다.
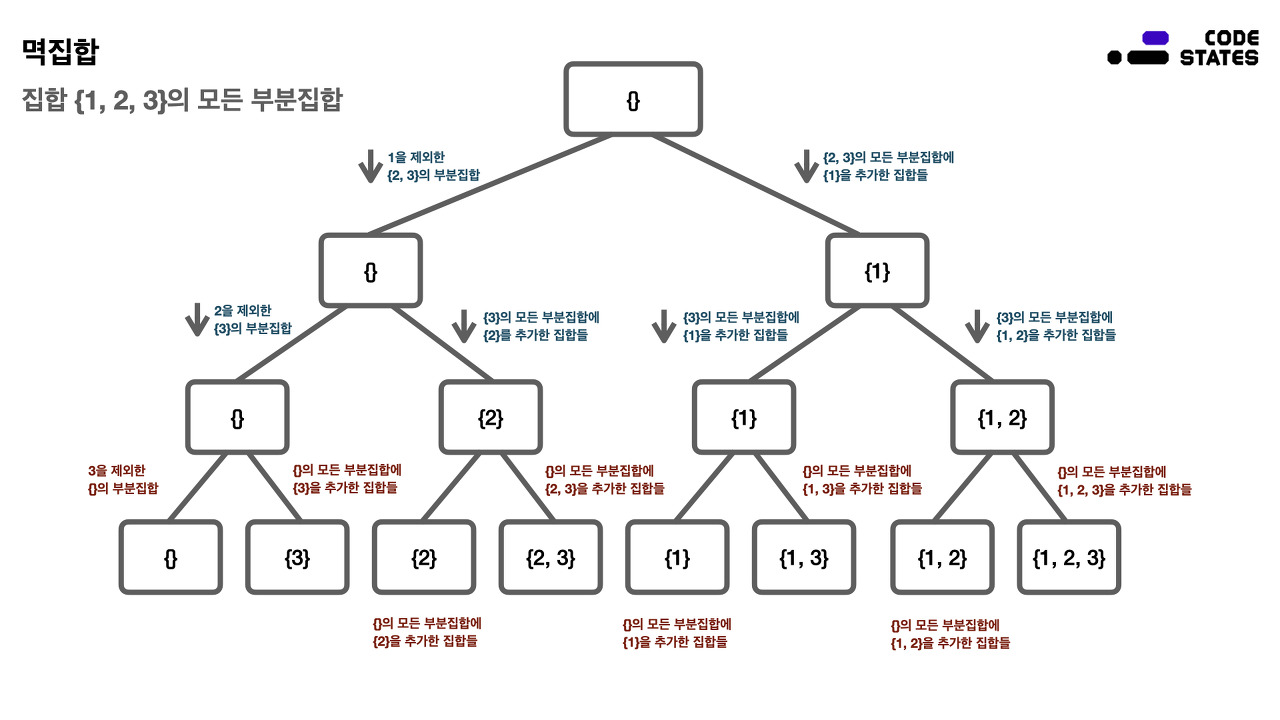
멱집합 문제는 트리 문제는 아니다. 그림은 이해를 돕기 위해 사용되었다.
멱집합을 구하는 방법에서 각 단계를 유심히 살펴보면, 순환 구조를 띠는 것을 확인할 수 있다. 여기서 순환구조는 임의의 원소를 제외하면서 집합을 작은 단위로 줄여나가는 방법이다. 따라서, 문제를 작은 단위로 줄여나가는 재귀를 응용할 수 있다. 예를 들어 PowerSet 이라는 멱집합의 개수를 리턴하는 함수를 작성한다면, PowerSet 함수에서 자기 자신을 호출하며 문제를 더 작은 문제로 문제의 크기를 줄여 해결할 수 있다. 문제가 가장 작은 단위로 줄어들고, 함수가 리턴될 때 카운트를 올리는 방식으로 멱집합의 개수를 구할 수 있다.
멱집합 예제 - Power Set
집합 S가 있을 때, Power Set인 P(S)는 집합 S의 거듭제곱 집합으로, S의 모든 부분 집합의 집합을 의미한다.
예를 들어 S가 {a, b, c} 으로 요소가 3개일 때, P(S)는 {{}, {a}, {b}, {c}, {a,b}, {a, c}, {b, c}, {a, b, c}} 으로 요소가 8개임을 알 수 있다.
즉 S에 n개의 요소가 있다면 P(S)에는 2^n의 요소가 있음을 의미한다.
Example
Set = [a, b, c]
power_set_size = pow(2, 3) = 8
Run for binary counter = 000 to 111
Value of Counter Subset
000 Empty set
001 a
010 b
011 ab
100 c
101 ac
110 bc
111 abc이제 알고리즘 로직을 보도록 하자.
Input : Set[], set_size
- 모든 집합의 크기를 가져온다. => power_set_size = pow(2, set_size)
- 0에서부터 power_set_size까지의 반복문 실행
- i = 0에서 set_size까지 크기를 지정해 반복문을 돌린다. 그리고 집합에서 i번째 요소에 해당하는 하위 집합을 출력한다.
- 하위 집합을 구하면 개행을 통해 집합을 구분한다.
주어진 집합 S에 대해 거듭제곱 집합은 0과 2^n-1 사이의 모든 이진수를 생성하여 찾을 수 있다. 여기서 n은 집합의 크기이다. 예를 들어 집합 S {x, y, z}에 대해 0부터 2^3-1까지의 모든 이진수를 생성하고, 생성된 각 숫자에 대해 해당 숫자의 집합 비트를 고려하여 해당 집합을 찾을 수 있다.
아래는 위에서 소개한 접근 방식을 구현한 것이다.
let inputSet = ['a', 'b', 'c'];
function powerSet (arr) {
const result = [];
function recursion (subset, start) {
result.push(subset);
for(let i = start; i < arr.length; i++){
recursion([...subset, arr[i]], i+1);
//이렇게도 구현할 수 있습니다.
recursion(subset.concat(arr[i]), i+1);
}
}
recursion([], 0);
return result;
}
poserSet(inputSet);Output
[
[],
[ 'a' ],
[ 'a', 'b' ],
[ 'a', 'b', 'c' ],
[ 'a', 'c' ],
[ 'b' ],
[ 'b', 'c' ],
[ 'c' ]
]위의 powerSet 로직은 재귀함수를 이용하여 구현한 것이다. 재귀함수에 부분집합을 만들기 위한 빈배열과 시작할 숫자를 지정한다. 이어 숫자가 커지게끔 하면서 중심 로직인 반복문을 돌려 부분집합을 만든 뒤, 최종적으로 배열 result에 push한다.
'코드스테이츠 SEB FE 41기 > Section 별 내용 정리' 카테고리의 다른 글
| 정규표현식 (0) | 2022.12.12 |
|---|---|
| section4/Unit11/[자료구조/알고리즘] 코딩 테스트 준비 (1) | 2022.12.09 |
| section4/Unit10/[Deploy] CI/CD (0) | 2022.12.08 |
| section4/Unit10/[Deploy] CI/CD (0) | 2022.12.07 |
| section4/Unit9/[Deploy] Amazon Web Service(AWS 배포) (0) | 2022.12.06 |


